Michael Paquette1, Chantal M.W. Tax2, Cornelius Eichner1, and Alfred Anwander1
1Neuropsychology, Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany, 2CUBRIC, School of Physics, Cardiff University, Cardiff, United Kingdom
1Neuropsychology, Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany, 2CUBRIC, School of Physics, Cardiff University, Cardiff, United Kingdom
Gradient non-linearities distort the gradient waveform used for b-tensor diffusion encoding. We derive the closed-form formula of the voxelwise B-tensor under gradient non-linearity, independent of the choice of gradient waveform.
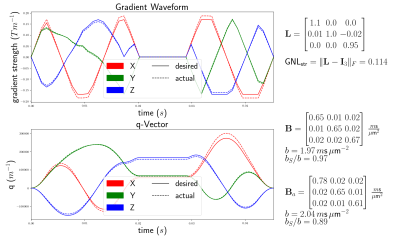
Figure 1: Gradient waveform and q-vector for a spherical B-tensor ($$$b = 1.97\,m\text{s}/\mu\text{m}^2$$$, $$$\text{G}_{\text{max}}=170\,m\text{T}/\text{m}$$$). The dashed lines show the actual curves under the effect of a "strong" GNL tensor $$$\mathbf{\text{L}}$$$ (approximately the top 10% of voxels for typical brain at Connectom scanner are at least this affected). The actual B-tensor $$$\left(\mathbf{B}_a\right)$$$ has an inflated b-value and is not spherical.
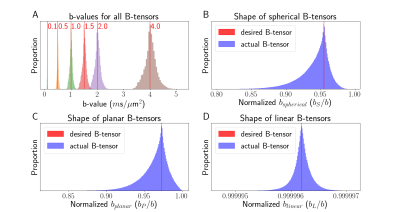
Figure 3: Deviations from the desired B-tensor acquisition scheme described in the experiment section for full brain volume incorporating GNL. (A) Max-normalized histogram for each b-value, showing a distribution of b-values up to $$$\pm 15\%$$$ around the desired b-values (vertical red lines). (B - D) For each type B-tensor shape (spherical, planar, linear), we show the spread of their respective normalized shape metrics $$$\left(b_S/b,\,b_P/b,\,b_L/b\right)$$$8.
